转载自张建华的博客, 原文链接: http://www.jeffzhang.cn/Do-we-need-FAHP/.
yaahp曾经规划过模糊层次分析法(Fuzzy Analytic Hierarchy Process, FAHP)功能, 但还没有开发完成就取消了, 原因是我认为不需要FAHP.
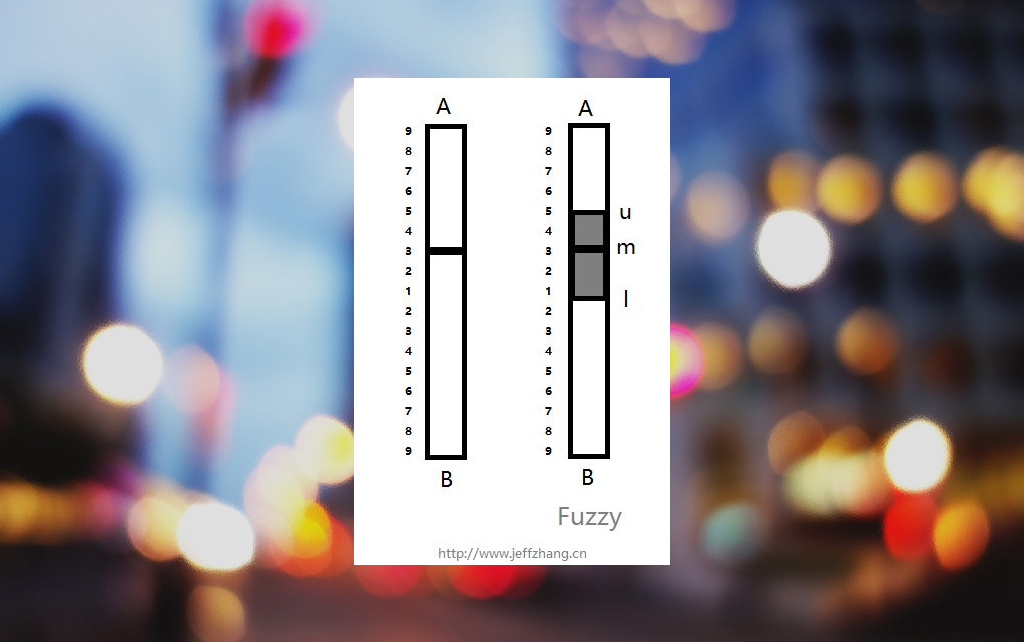
注: 这里所说的模糊层次分析法(FAHP)指判断矩阵中的两两比较数据使用模糊数表示, 例如三角模糊数(3,5,6), 而不是AHP与模糊综合评价法(FCE)结合的综合评价方法. yaahp提供了结合AHP和FCE的综合评价方法.
引言
关于模糊层次分析法的研究很多, 可以检索到大量的的相关文献. 但是AHP理论提出者Thomas L. Saaty对此有不同的意见, 并分别于2006年[1], 2007年[2], 2010年[3]发表三篇论文讨论了FAHP的有效性. 此外, 合肥工业大学的朱克毓博士在其攻读博士学位期间对此问题进行了深入研究[4-6].
希望进一步了解可以查阅参考文献.
FAHP提出
FAHP提出时主要针对AHP的两个”问题”:
- 判断矩阵一致性检验缺乏科学依据并且过程繁琐;
- 1-9标度不能反映人的主观判断的模糊性;
第一个问题确实是存在的, 但FAHP也没有解决; 对于第二个问题, FAHP引入进一步的模糊化处理, 使问题复杂化, 但没有获得更好的效果, 相比起来, 1-9标度的模糊处理反而显得更加简单有效.
Saaty对于FAHP的观点
Saaty的三篇论文从几个角度讨论了FAHP的有效性.
- 缺乏数理有效性
- 模糊化判断矩阵意义不大
- 改善一致性但没有考虑结果的有效性
缺乏数理有效性
理论论证, 参见参考文献.
模糊化判断矩阵意义不大
因为1-9标度中各个标度对应的是要素两两比较的”同样重要”, 比较重要”,”明显重要”等关系, 已经是模糊的表示, 例如”A方案比B方案明显重要”就是模糊的判断.
FAHP将这些已经是模糊的数据进一步模糊化, 只是产生更大的不确定性, 并不是模糊性从无到有, 意义并不大.
改善一致性但没有考虑结果的有效性
进一步的模糊化虽然改进了判断矩阵的一致性, 但没有考虑结果的有效性, 并不能确定能够获得更好的决策结果.
yaahp之前版本除了1-9标度外, 还提供一种指数标度. 后来的版本去掉了这种指数标度, 也是出于类似的考虑, 使用这种指数标度虽然可以增强判断矩阵的一致性, 但对决策结果的改善没有帮助, 反而增加很多计算和操作的复杂性.
需要FAHP吗?
不能认为FAHP有效地解决AHP存在的问题, 但是可以确定FAHP增加了复杂度, 所以我认为不需要FAHP.
参考文献
[1] Saaty T L. There is no mathematical validity for using fuzzy number crunching in the analytic hierarchy process[J]. Journal of Systems Science and Systems Engineering, 2006, 15(4): 457-464.
[2] Saaty T L, Tran L T. On the invalidity of fuzzifying numerical judgments in the Analytic Hierarchy Process[J]. Mathematical and Computer Modelling, 2007, 46(7): 962-975.
[3] Saaty T L, Tran L T. Fuzzy judgments and fuzzy sets[J]. International Journal of Strategic Decision Sciences (IJSDS), 2010, 1(1): 23-40.
[4] Zhü K. Fuzzy analytic hierarchy process: Fallacy of the popular methods[J]. European Journal of Operational Research, 2014, 236(1): 209-217.
[5] 朱克毓, 杨善林. 关于 Saaty 对模糊逻辑不适用于 AHP 观点的评述[J]. 系统工程理论与实践, 2014, 34(1): 197-206.
[6] 朱克毓. 模糊 AHP 的无效性与基于几何加权的 AHP 方法研究[D]. 合肥工业大学, 2012.